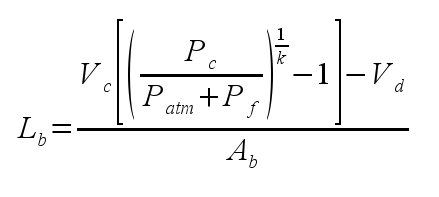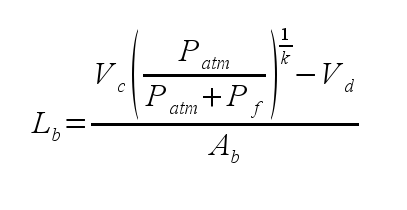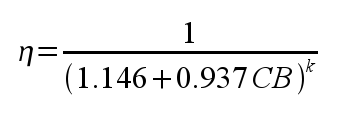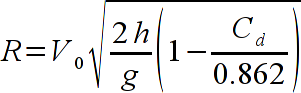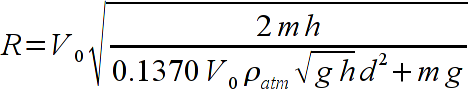28 replies to this topic

[Doom]

I produced a series of tables that are useful in designing air guns. Through these tables one can find optimal barrel lengths, predict performance, and do a number of other things, given that one understands how to use the tables.

What are these tables useful for?

1) Predicting performance of air guns.
2) Finding ideal barrel lengths.
3) Calculating critical gun and dart parameters (chamber volume, barrel length, minimum valve efficiency, etc.) given a desired muzzle velocity and dart mass. The parameters describe a system at peak efficiency, so pumping effort is reduced to a minimum.
4) Many other possibilities. The tables are intentionally general.

Below are the tables in different formats with explanations.

http://trettel.org/n...dm/pneu-eng.xls
http://trettel.org/n...dm/pneu-eng.ods
http://trettel.org/n...m/pneu-eng2.csv

I'm receptive to questions and suggestions.

The tables show energy efficiency at certain gun configurations. This essentially is how much of the input energy is translated into dart kinetic energy. 1 is the maximum. 0 means that the dart never leaves the barrel. As you can notice, higher pressures have higher peak efficiencies.

IMPORTANT NOTES:

These tables give you a rough idea of what configurations are optimal, nothing more. The tables are not exact. Always do some tests to verify the table's result. A chronometer or ballistic pendulum is required. Also, outside of what assumptions are made (nearly no friction, very little dead space, no air cylinders, valves that open very quickly, etc.), I wouldn't expect any accuracy.

These tables only apply to air guns. If the ratio of specific heats is not 1.4 or near 1.4, the tables are probably inaccurate, especially at lower C:B ratios (like 0.2:1). These tables do not apply to spring guns either.

Edited by Doom, 01 June 2010 - 04:05 PM.

[Mr BadWrench]

The only real problem is that you saved it in a format only about 10% of the members can read.

Anyone who is interested, I suggest you go to www.openoffice.org and download the LGPL licence
Openoffice.org 3 software.. if you are in school you NEED it anyways.

Don

[Doom]

Thanks for pointing that out Badwrench. See the updated post with versions in multiple formats. I'll suggest OpenOffice.org too (It's what I use).

By the way, SpudFiles has a bit more about what C:B ratio means, though they focus mainly on combustion guns: http://www.spudfiles...to_barrel_ratio

I'll give two examples of how to use these tables below. I hope these examples illustrate how useful the tables could be. All you need is a copy of the tables, some paper, a pencil, and maybe a pocket calculator to design optimal air guns this way. (The testing part is separate from design.)

An example of how to use the tables

Let's say that you are modifying a gun. You have little control over the chamber volume or the weight of your darts, but you can control the pressure and the barrel length.

You measure the weight of your darts at 1.0 grams and through geometry you estimate that your chamber volume is 2 in^3 (32.7 cm^3). You determine that the highest safe pressure the gun can operate at is 45 psig, which is about 4 atmospheres in absolute pressure.

Looking at the top left table you see that at Pc*(0) = 4, the optimal C:B ratio is 0.661:1. So, you solve the equation CB = Vc / Ab * Lb. 0.661 = 2 / 0.221 * Lb solved returns Lb = 13.69 inches.

Now you have to check to see if the dart is heavy enough for the top left table to apply. The valve efficiency isn't known, so we'll assume that it's low at 0.2. Looking at the table for Pc*(0) = 4 we can see that the efficiency saturates at around md* = 250. We can calculate what md* for our dart is. md* = md / Vc * rho_atm. rho_atm = 0.0012 g / cm^3 and Vc = 32.7 cm^3. So md* = 1 / (0.0012 * 32.7) = 24.9.

So the darts aren't heavy enough for the efficiency is the top left table to apply, but the optimal C:B ratio is still about right, so the optimal barrel length about is about right too.

If the valve efficiency was about 0.4, then the critical md* value is about 60. Most good valves probably have an efficiency of about 0.4. For a valve efficiency of 0.8, which is possible, but not likely, the critical md* valve is about 40 (24.9 isn't too far off, though). This shows both the value of having a good valve and that heavy projectiles can usually absorb more energy; things we knew without the tables.

Another example

Let's say that you are planning a homemade. You want a gun that shoots a 1.5 gram dart at 200 ft/s (61 m/s). You are comfortable pumping up to about 60 psig (Pc*(0) = 5).

From the top left table you see that eng = 0.49 and CB = 0.51 for Pc*(0) = 5. The eng equation can be rewritten to solve for Vc.

Vc = (0.4 * 1.5e-3 kg * (61 m/s)^2) / (2 * 101325 Pa * 0.49 * (5 - 5^0.714)) = 12.2 cm^3 = 0.744 in^3

You should note that 0.744 in^3 seems really small. It is! That's why you want to find the optimal configuration; it can reduce the amount of energy you need to exert a lot.

So with Vc known, we can use the optimal C:B ratio to find the barrel length. Lb = Vc / Ab * CB = 12.2 / 1.43 * 0.51 = 16.7 cm = 6.6 inches.

And md* = 1538, which is pretty big, so an extremely high flow valve isn't necessary. Something like the Clippard JEV-F2M2 valve I use would be very adequate.

Edited by Doom, 29 May 2010 - 03:14 PM.

[Daniel Beaver]

Thanks for posting these. Your post in the barrel length thread mentioned that you were assuming an air-tight fit between the dart and the barrel. I assume that is true of these tables?

[Doom]

Yes. The model assumes that no leaks exist. From my understanding of the problem, this is okay for the slight amount of air loss from around a dart. If you find the tables are consistently wrong then this might be something to evaluate in the future. Let me know if that is the case.

I'll try to make assumptions like that more clear in an edit of the spreadsheet.

Another not obvious assumption: The gas starts are atmospheric temperature. Is this a good assumption? Intuitively, it depends on how much time elapses between filling the gas chamber and firing. I compared the two possibilities (hot gas from after pumping vs. atmospheric temperature gas) and found that the efficiency changed only a negligible amount, so this should be a good assumption for at least most cases.

Edited by Doom, 09 May 2010 - 05:20 PM.

[moosa]

Doom, on May 9 2010, 05:20 PM, said:

Yes. The model assumes that no leaks exist. From my understanding of the problem, this is okay for the slight amount of air loss from around a dart. If you find the tables are consistently wrong then this might be something to evaluate in the future. Let me know if that is the case.

I'll try to make assumptions like that more clear in an edit of the spreadsheet.

Another not obvious assumption: The gas starts are atmospheric temperature. Is this a good assumption? Intuitively, it depends on how much time elapses between filling the gas chamber and firing. I compared the two possibilities (hot gas from after pumping vs. atmospheric temperature gas) and found that the efficiency changed only a negligible amount, so this should be a good assumption for at least most cases.

Given the amount of variables that still exist, my inclination is that it would be more "efficient" to guess and check for barrel lengths, and probably without any resulting loss in performance over using your tables. Given how rigorous you've attempted to be here, it would be a good idea to evaluate for yourself the actual consistency, accuracy, and overall benefit of using your table method over the conventional means before you pin this as "useful." Unless others with as much scientific vigor happen around here and believe it may be worth their time to check your work, this may never become "useful" in that sense. And even if you could account for as many variables as possible, there's always variation within the components of the blasters themselves, which you have no control over and would further skew actual results.

Do you see where this is going? It's like the Uncanny Vally; the more vigor you put into trying to achieve true accuracy, the more rapidly that ideal separates itself from you. I don't think you're going to get any significant improvements in results via this method compared to conventional methods (let alone the extra work involved and whether or not anyone cares about 5 extra feet). I do appreciate the effort, and realize you're not making any big claims here, but I don't want people to come in here and be dazzled by all the mathematics and think this is the Barrel Length Guide thread 2.0, this time made by a Nerf god. I don't mean this to sound harsh, but you did sort of bring it on yourself.

[Doom]

Thanks for the comment moosa.

Bob, that is a good summary of what I've tried to say. Thanks for stating it more explicitly than I have.

Now for my latest novel...

Quote

Given the amount of variables that still exist, my inclination is that it would be more "efficient" to guess and check for barrel lengths, and probably without any resulting loss in performance over using your tables.

These tables are far more powerful than testing due only to the time involved in testing. At worst these tables reduce the number of tests to perform. There also aren't too many variables in the pneumatic problem and a number of assumptions can be made that are valid in general.

What is the conventional way to make an air gun perform at peak efficiency at a certain level of performance? One might make a gun of reasonable dimensions and keep increasing pressure until the desired performance is reached. This doesn't result in an optimal configuration, so to get an optimal configuration, one has to start adjusting other parameters. This gets very complicated; these tables provide a shortcut.

Finding the ideal barrel length for a gun of a fixed gas chamber volume (i.e. a modified gun) is a little more straightforward. But this often will result in configurations where the darts are too light for peak efficiency. The tables provide insight here to not only reduce testing time, but to also let you know that your gun likely will perform better if you increase dart mass.

As for the limitations of the model and this approach, the model make a number of assumptions that are valid for guns people would want to use. Ideally, valves open quickly, dead space is small, and there are no leaks. If one is going to take the time to design an efficient gun, surely these assumptions would be valid, so I see no reason to include other assumptions in a relatively simple table like this.

The assumptions I've made in this model are valid for at least 90% of good performing Nerf air guns. Additional variables aren't necessary.

Quote

Given how rigorous you've attempted to be here, it would be a good idea to evaluate for yourself the actual consistency, accuracy, and overall benefit of using your table method over the conventional means before you pin this as "useful."

I'll admit that I have not had the time to verify the accuracy of the tables. This will be done when I have the time. I'm very reasonably confident in the tables, however, as simpler simulations I've written were plenty accurate and I checked my work many times before implementing the simulation.

Quote

I don't think you're going to get any significant improvements in results via this method compared to conventional methods (let alone the extra work involved and whether or not anyone cares about 5 extra feet).

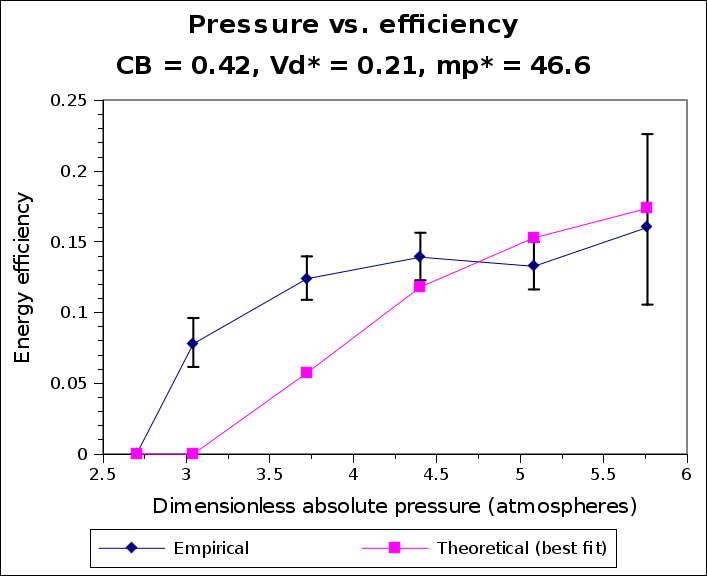
The performance increase can be very substantial. Most Nerf guns have efficiencies of less than 20%, even with optimized barrel lengths. A quick glance at my table shows that efficiencies over twice that are possible. This does far more than increase range by 5 feet. I'm not even interested in improving range; I want to keep range constant while reducing the amount of energy I put in the gun. That's practically impossible outside of simulation, as I've tried to explain above.

Quote

And even if you could account for as many variables as possible, there's always variation within the components of the blasters themselves, which you have no control over and would further skew actual results.

Uncertainties in measurements and the fact that we can't control for everything do make test results variable. But, this is a fact of empirical measurement, and is no reason not to use a model.

Quote

I don't want people to come in here and be dazzled by all the mathematics and think this is the Barrel Length Guide thread 2.0, this time made by a Nerf god.

Me neither. In fact, I waited a few weeks before posting this because I wasn't sure how people would react. I'm thankful that no one has accepted this as some sort of dogma.

Also, if it was unclear, my post in the recent barrel length thread was partly a joke.

Edited by Doom, 15 May 2010 - 06:26 AM.

[Draconis]

*Reads articles*

*Accepts as dogma*

*Begins worshiping new lord, Doom the mathematically verbose*

[moosa]

Could you do me a favor (and this is not simply for my sake but for everyone who may come across this thread) and make it abundantly clear what exactly it is you've set out to accomplish here? It's kind of one of those things where someone comes into this and starts reading, thinks "oh this sounds like it might be something useful," and then a couple paragraphs later they have no idea what's going on, or what exactly all of this could mean to them. I hope you see what I'm trying to say.

[Fome]

I'm still not sold on how this is necessary to enjoy the hobby. At all.

Even if you did get a blaster to shoot 50 darts 100 feet with one pump, it'd get banned instantly. The thing about creating/modifying nerf guns is that you have to be highly cognizant of what other people are using. If your blaster is way more powerful than every other blaster on the field, then noone is going to want to play with you.

If you enjoy the math, more power to you. I can see why some people would get a kick out of this stuff. However, there really isn't much of a reason for anyone to crunch the numbers beyond that, considering that a simple "guess and check" can get you all the performance you need to actually go shoot people.

I know this post seems negative, Doom, but I really do appreciate the thought you put into this. My big question is "why do this?"

[TantumBull]

Fome, I think what Doom is saying is that he did this not to get the max range out of a set configuration, but to get the most efficency from a variable configuration out of a set range, thus lowering the amount of energy needed to prime/pump/ready a blaster.

Doom, thanks for the crunching. This is some sweet stuff. I'll probably be checking out BAGS pretty soon as well as I'm planning on starting a small bore/high pressure spud gun.

[Doom]

Quick question: Who would be interested in tables for spring guns?

moosa said

Could you do me a favor (and this is not simply for my sake but for everyone who may come across this thread) and make it abundantly clear what exactly it is you've set out to accomplish here?

Good idea. I've put three possible uses of the tables in the original post. Thanks.

Fome said

I'm still not sold on how this is necessary to enjoy the hobby. At all.

Where have I said that this is necessary to enjoy the hobby? I've enjoyed the hobby for 6+ years without these tables.

Fome said

Even if you did get a blaster to shoot 50 darts 100 feet with one pump, it'd get banned instantly. The thing about creating/modifying nerf guns is that you have to be highly cognizant of what other people are using. If your blaster is way more powerful than every other blaster on the field, then noone is going to want to play with you.

One reason I've made these tables accessible is so that I'm not the only one with finely optimized guns. I'm not in an arms race; I'm here for fun, and that means ideas are shared. Bring it on!

This, to me, seems like an argument against anything that improves performance. Why modify guns? That's not "necessary" to have fun and some people might not like it!

I think one pump air guns that get 100 feet of range are possible, but getting more than two shots is probably not possible.

I'd like to reiterate that I intend to set performance (i.e. power) first and find the remainder of the gun parameters from there. I'm not interested in making a more powerful gun. As TantumBull said, I'm looking to minimize pumping effort.

Also, I really doubt the improvements are going to be so dramatic that my guns will be banned. I would notice that pumping requires less effort. I doubt anyone else would notice.

Fome said

However, there really isn't much of a reason for anyone to crunch the numbers beyond that, considering that a simple "guess and check" can get you all the performance you need to actually go shoot people.

If you just want to shoot people with Nerf darts, then these tables aren't for you.

I think you fundamentally misunderstand the point of these tables. Nowhere did I say these are necessary for everyone. They are an option to help people design Nerf guns. Nothing more.

TantumBull said

Doom, thanks for the crunching. This is some sweet stuff. I'll probably be checking out BAGS pretty soon as well as I'm planning on starting a small bore/high pressure spud gun.

Good to hear you like the tables.

BAGS at the moment is a lot harder to use than GGDT, so I'd suggest GGDT unless you can't run GGDT. Down the road I'll add a GUI to BAGS.

Edited by Doom, 15 May 2010 - 11:35 AM.

[phillypretzel]

Thanks for posting these tables, Doom, and the time and thought you have given them. Despite what others may think of the idea of actually engineering a nerf blaster, as opposed to splooging hot glue and e-tape all over the place, I find this type of information extremely useful (assuming it's remotely accurate). The whole idea of modding a nerf gun is to make it more efficient, increased efficiency results in better ranges, more shots per tank, less pumping, and a higher ROF. At best, these tables could save time (instead of trial and error) in tuning the barrel length to the air tank, and at worst, at least give you a reasonable starting point.

I will use these tables to make barrels for an AT3K, Signal Launcher (BBBB tank), and a Titan (the 3 air guns I have on hand), and post the results here. I will compare the range differences to the (mostly arbitrary) barrel lengths I have been using. In doing this, I will have to determine the tank volume, as best I can (I have slide calipers, not a micrometer), and will post that VERY useful information here as well. Perhaps the rest of the community can jump in here and we can compile a list of airguns, their blast chamber volume, approximate operating pressure, and their optimal barrel lengths.

This could prove to be a very useful reference thread.

And perhaps, as I help carry the shining torch of science and progress forward, I will figure out how to post something with fucking italics. Motherfucker.

Edited by phillypretzel, 15 May 2010 - 11:38 AM.

[moosa]

phillypretzel, on May 15 2010, 12:37 PM, said:

Perhaps the rest of the community can jump in here and we can compile a list of airguns, their blast chamber volume, approximate operating pressure, and their optimal barrel lengths.

I'm sorry but we've already been over this. There are too many variables to make posting a list of optimal barrel lengths a legitimate idea. Blast chamber volume is different, of course, as that's pretty much constant. And operating pressures, maybe, but that can be quite variable too, as I understand it.

Doom, I think the key words to describe the real purpose of what you're doing here are optimization and efficiency. You seem to put a focus on barrel lengths in your description and topic title, which could be a little misleading, as that seems to be only a small part of whats going on here. If the ONLY thing someone is interested in is finding the right barrel length for their blaster, I believe the "guess and check" method is still much better than trying to use these tables. If, however, one is interested in accounting for all of these other variables in their blaster at the same time, or is just interested in other variables besides barrel length, THEN the tables become useful. Does that make sense to you as well?

PS, I appreciate your maturity in responding to this feedback. It's refreshing to be able to discuss something intellectually without people unnecessarily taking things personally.

Edited by moosa, 15 May 2010 - 09:34 PM.

[Doom]

phillypretzel, I'm glad to hear you'll use the tables and am even happier to learn that you'll help validate them.

Be as descriptive as possible. Provide dart mass (to the tenth of a gram, at the least), dead volume, chamber volume, minimum contraction area, operating pressure, how well the darts fit (Can the barrel be used as a blowgun?), ideal barrel length, etc. If any of these are estimated, make that clear. Local atmospheric conditions might be helpful too. Weather.gov will give you both local atmospheric temperature and pressure if you live in the US.

Using water to measure volumes is a good trick, too, if you weren't aware.

If possible, also test muzzle velocities. A chronometer is somewhat expensive ($90, at most), but it's also very useful. I have one for Nerf and spud gunning.

moosa said

I'm sorry but we've already been over this. There are too many variables to make posting a list of optimal barrel lengths a legitimate idea. Blast chamber volume is different, of course, as that's pretty much constant. And operating pressures, maybe, but that can be quite variable too.

There are many variables, yes, but there's no harm from posting detailed descriptions of guns and their optimal configurations given that it is obvious that your results may vary even if your gun is very similar. Also, in the other barrel length thread, I noted that such a listing would be useful as a starting point for testing if the configuration is similar enough.

Obviously, we need to discourage thinking that all guns are the same, so I understand where you're coming from.

I'll give another reason I'd like to see something like that. If others posted information about their gun configurations, I'd have a better idea of what is often used and what results are seen. I could then adjust the tables to be more useful and/or accurate in general.

I'll ask this again: Is there any interest in similar tables for spring guns?

Edited by Doom, 15 May 2010 - 09:49 PM.

[moosa]

Doom, on May 15 2010, 10:28 PM, said:

Obviously, we need to discourage thinking that all guns are the same, so I understand where you're coming from.

Not only the guns, but the barrel material/dimensions, the dart size/fit, and the pressures you're pumping to. And obviously there's no possible way to account for all the differences in every individual mod. As long as its not a list that anyone thinks they can simply look up an optimum length for their blaster's barrel, then I don't see a problem with it if you find it useful for other means. I think we just really need to get away from this idea of being able to look up barrel lengths.

[Doom]

Want an equation for ideal barrel length for air guns? Look below!



This equation applies for md > 100 * rhoatm * Vc (approximately). The heavier the dart, the more accurate this equation is (technically this equation applies for md = infinity). md could be lower than that value and this equation could still apply. Check the tables to be certain.

All pressures are absolute.

Lb is barrel length
Vc is chamber volume
Pc is chamber pressure
Pf is "pressure of friction"
k is the ratio of specific heats (1.4 for air)
Vd is "dead volume"
Ab is the cross sectional area of the barrel (i.e. pi * d^2 / 4)
md is dart mass
rhoatm is atmospheric air density

This equation matches my numerical results nearly perfectly. While I did not derive it from the ODEs used for my simulation, I believe it is accurate and correct.

I'm going to work on the springer tables and equation now...

Edit: By similar logic, the equation below should apply for springers.



Vc is the volume of the plunger tube up to the plunger head (I should use a different variable name)

I haven't checked the spring equation against simulations or empirical data, so take it for what it's worth.

Edited by Doom, 31 May 2010 - 06:37 PM.

[Blue]

Can you show how to do an example with a common gun like the AT2K or BBBB?

[Split]

Doom, you know, assuming no dead space and no "breaking point" pressure, the springer works out to "Volume of the barrel = volume of the chamber," which is what people have been trying for years, but it yields results that are too long... That's why they added the "arbitrary" coefficient on the front - as a sort of "inefficiency multiplier." I believe you responded unfavorably to one of those threads.

[moosa]

Blue, on May 31 2010, 07:47 PM, said:

Can you show how to do an example with a common gun like the AT2K or BBBB?

You just find the values of all the variables, and then use algebra to solve and hope that the result is accurate enough to warrant all the time you just spent.

[Doom]

Blue, on May 31 2010, 07:47 PM, said:

Can you show how to do an example with a common gun like the AT2K or BBBB?

I've already provided some examples of how to use my tables in my second post of this thread. This makes the calculation of ideal barrel lengths a little easier.

Here's how to use this in general:

1) Realize that this is only a starting point for testing. If you use this equation without testing and checking against the tables I've provided, you are doing it wrong.

2) Measure the mass of your darts. If they are below the critical mass I listed, then this equation may not apply. Use the tables and the procedure I outlined earlier to check if the equation applies.

3) Determine the diameter of your barrel. Barrels for micros are about 0.53 inches in diameter. Use the equation for the area of a circle to calculate the area of the barrel (Ab). For micros this is about 0.221 inches^2.

4) Approximate the volume of the gas chamber with geometry. I can't do this for you.

5) Approximate the amount of dead volume using geometry. I can't do this for you.

6) If you can blow the dart down the barrel, use 0.25 psi as Pf. If you can't blow the dart down the barrel, figure out another way to measure the force required to move the dart.

7) Plug the numbers into the equation and see what it returns.

8) Do some tests with barrels of lengths around the estimated ideal length to see what's ideal.

Split, on May 31 2010, 07:56 PM, said:

Doom, you know, assuming no dead space and no "breaking point" pressure, the springer works out to "Volume of the barrel = volume of the chamber," which is what people have been trying for years, but it yields results that are too long... That's why they added the "arbitrary" coefficient on the front - as a sort of "inefficiency multiplier." I believe you responded unfavorably to one of those threads.

Edit: I think I misread Split here, but I'll leave my comments.

I noticed that. Three things:

1) I'm not certain the springer equation is even approximately right. The springer equation would have a dart mass restriction similar to the pneumatic case. A second restricting assumption made is that the plunger hits the end of the plunger tube when the projectile leaves. Is that realistic? I don't know, but it seemed reasonable. Before I criticized boltsniper for assuming that was true. You can call me a hypocrite for making the same assumption. I'm reasonably certain that it's at least approximately correct, but, I haven't made sure yet.

Wait for numerical and empirical verification before using that equation. I posted it primarily so someone could test or critique it (as you are doing).

2) No dead space and no friction are atypical conditions, so I wouldn't expect that special case of the equation to be right for most guns. I'd estimate that the pressure of friction for springers is typically from 5 to 30 psi. This is not insignificant, and it reduces the barrel length. You can rearrange the equation to find the pressure of friction if you know the ideal barrel length, plunger tube volume, and dead volume. Note that dead space also reduces the barrel length. This fits well with my expectations.

3) The "efficiency coefficient" that you are referring to was arbitrarily set. They also just guessed that there would be relationship between the volumes. They had no reason to believe there was a relationship between those parameters. They also used one constant and assumed it worked for all situations. My criticisms were about the unjustified assumptions made. My equation is based on theory (adiabatic process relationships, specifically) and the results of numerical simulations; this reduces the guesswork substantially.

I'll post a derivation of the air gun equation tomorrow. As I've mentioned, it can be derived from some (reversible) adiabatic process relationships.

Edited by Doom, 01 June 2010 - 03:40 PM.

[Doom]

I'm reasonably certain that higher static friction in the initial part of the barrel would not affect the ideal barrel length equation, but would affect the critical dart mass that determines if the ideal barrel length equation provided is valid. It would work in the same way that higher flow valves do.

The ideal barrel length formula is independent of parameters like initial friction, etc., because it finds where the gas stops expanding. The friction at the beginning of the shot doesn't factor into that equation. The chamber pressure and barrel pressure are approximately the same for heavy projectiles and high flow coefficients, which is why the critical dart mass is lower for high flow coefficients.

I'll post the derivation of this eventually.

Incidentally, using the same math one can calculate the efficiency, but it's always 100%. This was why I was wary of any method similar to this before, but I can't argue with its fit to my C:B ratio data.

So, to find an equation for the efficiency for the special case where the air blaster barrel length equation applies, I manipulated the data I had a bit until I found a linear relationship and I did a linear regression. The equation below fits the data very well (R^2 = 0.999). I have no idea if this relationship applies more generally; I need to run some more numerical simulations, but this seems to be reasonable.



Again, this does not apply in general. The same conditions on the use of the earlier ideal barrel length equation apply.

I'll update the spreadsheet with this information, some clarifications, and a correction (eng was supposed to be eta...).

Edit: I want to respond to some insightful comments by moosa that I had missed.

moosa said

Doom, I think the key words to describe the real purpose of what you're doing here are optimization and efficiency. You seem to put a focus on barrel lengths in your description and topic title, which could be a little misleading, as that seems to be only a small part of whats going on here. If the ONLY thing someone is interested in is finding the right barrel length for their blaster, I believe the "guess and check" method is still much better than trying to use these tables. If, however, one is interested in accounting for all of these other variables in their blaster at the same time, or is just interested in other variables besides barrel length, THEN the tables become useful. Does that make sense to you as well?

PS, I appreciate your maturity in responding to this feedback. It's refreshing to be able to discuss something intellectually without people unnecessarily taking things personally.

I see where you are coming from. The stress on barrel lengths is somewhat necessary to get people to view the thread, and it's not what these tables do best as you've noted. I'll try to stress that these tables are best used to design air blasters from scratch rather than to optimize existing blasters.

Also, I'm not here to be right. I'm here to share what I've learned, and if I can learn more in that process, that's even better. Feedback is part of the learning process.

Edited by Doom, 01 June 2010 - 03:37 PM.

[Doom]

Since this is where I've posted a bunch of equations I figured this would fit here...

Want a somewhat simple way to estimate the flat range of a Slug dart with reasonable accuracy? Try the equation below.



This equation is based on the results of some testing I did back in 2009. My darts had the following characteristics on average:

mass: 1.06 g
Cd: 0.34
length: 2 inches
diameter: about 0.53 inches

Note that Cd is a parameter in the equation, however, this is probably not too accurate for Cds too far from 0.34.

Want a more general equation? The one below is just that. It's based on regressions made from the results of a simulation I wrote a month ago. This should be less accurate than the one above, but it is applicable in a wider range of areas (different masses and diameters, mainly). This equation applies only for Cd = 0.35 (slightly conservative for Slugs).



R is range
Cd is drag coefficient
V0 is muzzle velocity
g is gravitational acceleration
m is dart mass
h is height off the ground
rho_atm is atmospheric air density
d is dart diameter

I use both of the equations with a spreadsheet to predict how potential gun designs might perform. They aren't perfect, but they are helpful. As always, don't expect complete accuracy, but do expect to get a reasonable estimate of potential performance.

Edited by Doom, 11 July 2010 - 12:09 PM.

[Doom]

I did some testing with Clippard's JEV-F2M2 valve. The results are plotted below.



As you can see, the fit between the empirical data and the model for the closest realistic parameters is not the best. I attribute this to the simplicity of the model, especially with respect to valve dynamics. The valve is assumed to open instantaneously and remain open throughout the duration of the shot. The flow coefficient is assumed to be independent of the pressure drop across the valve. None of these assumptions are known to be realistic; I'd say that the first two are most definitely unrealistic for this valve.

Additionally, the flow coefficient of this valve was found to be extremely low (about 5% with the reference area being the barrel cross section). The model may not be accurate at such low flow coefficients; I noticed problems with stability of the simulation when the flow coefficient was this low. I suspect the flow coefficient is somewhat higher and the perceived best fit coefficient is only that; the perceived one.

What this means basically is that the model is inadequate for modeling a Nerf gun with this valve. I suspect better performing valves would be easier to model.

YakMan and I discussed this and some of his other worries about the valve yesterday on IRC and we both came to the conclusion that this one probably isn't the best choice for us. We'll investigate some alternatives.

[ZimZam93]

okay im sorry but i got a bit lost in all the math. But we are trying to find the perfect barrel length to find the furthest distance our type of darts can go? very interesting concept but for a kid with a C in geometry i think ill stick with guess and check

Edited by ZimZam93, 10 August 2010 - 01:00 AM.